Derivadas exponenciales y logaritmicas
Derivadas exponenciales y logaritmicas
Por: Samuel Nuñez
Estudiante de Ingenieria Industrial
Materia: Calculo diferencial
1.- Conocimiento personal.
a) Ideas aprendidas.
Continuando con el tema de las derivadas durante esta clase estuvimos analizando las reglas para resolver las derivadas de funciones con exponentes y logaritmicas.
1- Derivada exponencial
En referencia a esta regla de exponente se comprendio que la derivada de una funcion exponencial es igual a la misma funcion por la derivada.
Asi mismo si viene siendo el caso de ser la funcion de e a la x, vendria siendo igual quedando e con exponente x no cambiando en absoluto.
2- Derivada un logaritmo natural
d Ln u = du/u
Para el caso de la regla de una funcion con logaritmo natural se vio que la regla explica que se deriva solo el numero natural que acompañe al logaritmo y esto se divide entre el mismo numero natural.
de aqui se entiende que la derivada de un logaritmo natural de x, viene siendo = 1/x
tambien comprendi a mayor grado en esta clase que al igual que las reglas de funciones trigonometricas ademas de aplicar esta regla tambien pueden interactuar las reglas de derivada algebraicas ya sea cociente, producto, suma resta, cadena etc.
b) Aquello que se me dificulto.
Nuevamente reconozco mi dificultad para resolver derivadas de una funcion con raiz, asi como el saber hasta que grado pudo simplificar la ecuacion.
2. Conocimiento consultado.
Derivada de la función exponencial
La derivada de la función exponencial es igual a la misma función por el logaritmo neperiano de la base y por la derivada del exponente.
Derivada de la función exponencial de base e
La derivada de la función exponencial de base e es igual a la misma función por la derivada del exponente.
Derivada de e a la x
Para el caso especial
Tenemos que
Siguiendo la fórmula anterior
Se concluye que
Y así, decimos que la derivada de
es Derivada del logaritmo natural
Si la base del logaritmo es el número de Euler,
, entonces se logaritmo se conoce como logaritmo natural (o logaritmo neperiano). En este caso lo denotamos
Si
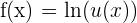, entonces la derivada del logaritmo natural es
donde ya estamos tomando en cuenta la regla de la cadena.
En particular, la derivada de
es
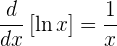
Derivada de un logaritmo de cualquier base
Sabemos que el logaritmo cumple con la siguiente propiedad:
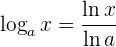
Por lo tanto, si derivamos la expresión anterior, tenemos:
Así, la derivada del logaritmo base
es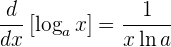
Si tomamos en cuenta la regla de la cadena, entonces la derivada es
Nota: en muchos casos es preferible aplicar algunas propiedades de los logaritmos antes de derivar. Por ejemplo, si tenemos
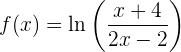
Entonces utilizamos la propiedad
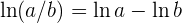para obtener: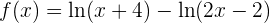
con lo que nos evitaríamos hacer la regla del cociente para las derivadas.
3.- Imagen
4. Videos
5.- Referencias
Conocimiento consultado: Derivadas de una funcion exponencial
Conocimiento consultado: Derivada de una funcion de logaritmo naturalImagenes:
https://www.superprof.es/apuntes/escolar/matematicas/calculo/derivadas/derivadas-logaritmicas.html
Comentarios
Publicar un comentario