Integración por partes.

Samuel Nuñez

Calculo integral

1.- Conocimiento personal.

a) Ideas aprendidas.

En esta clase se dio inicio a las técnicas de integración comenzando con el método de integración por partes.

una de las principales características revisadas en este temas fue su aplicación que en este caso es cuando dos funciones están multiplicando y/o dividiendo.

También, otro de las características los métodos de los cuales podemos hacer uso para un buen resultado como es el caso del termino I-L-A-T-E que por sus siglas es: Inversas, logarítmicas, Algebraicas, Trigonométricas y Exponenciales.

De igual forma parte de lo aprendió fue los pasos o procedimiento que se debe de tomar en cuenta durante su desarrollo:

Tomando en cuenta la formula de integracion por partes: ∫ udv= uv-∫ vdu

Identificar la u y dv para posteriormente obtener el valor de du y de v.

Aplicar la formula de integración por partes con los valores antes obtenidos

Sustituir valores entre otros aspectos hasta obtener el resultado.

B) Lo que se me dificulto

En primer instancia lo que mas se complico fue cuando se puede sacar un valor como el 2 por ejemplo de la integral y cuando no se puede sacar y aunque aun tengo dudas comprendi un poco mas que solo aplica cuando existe un valor de constante solo, sin formar parte de otra funcion como polinomio que fue el caso de parte de la tarea.

2. Conocimiento consultado.

Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula: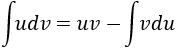

Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU).

Aunque se trata de un método simple, hay que aplicarlo correctamente.
Método:El integrando debe ser un producto de dos factores (si no lo es, podemos transformarlo para que lo sea).
Uno de los factores será u y el otro será dv.
Se calcula du derivando u y se calcula v integrando dv.
Se aplica la fórmula.

Escoger adecuadamente u y dv:

Una mala elección puede complicar más el integrando.

Supongamos que tenemos un producto en el que uno de sus factores es un monomio (por ejemplo x3). Si consideramos dv=x3. Entonces, integrando tendremos que v=x4/4, con lo que hemos aumentado el grado del exponente y esto suele suponer un paso atrás.

Normalmente, se escogen los monomios (o polinomios) como u para reducir su exponente al derivarlos. Cuando el exponente es 0, el monomio es igual a 1 y el integrando es más fácil.

Algo parecido ocurre con las fracciones (como 1/x). Si consideramos dv=1/x, tendremos v=log|x| y, probablemente, obtendremos una integral más difícil.

Como norma general, llamaremos u a las potencias y logaritmos y dv a las exponenciales, fracciones y funciones trigonométricas.

No cambiar la elección:

A veces tenemos que aplicar el método más de una vez para calcular una misma integral.

En estas integrales, al aplicar el método por n-ésima vez, tenemos que llamar u al resultado du del paso anterior y dv al resultado v. Si no lo hacemos así, como escoger una opción u otra supone integrar o derivar, estaremos deshaciendo el paso anterior y no avanzaremos.

Integrales cíclicas:

En ocasiones, tenemos que despejar la propia integral de la igualdad obtenida para poder calcularla. Por ejemplo, podemos aplicar integración por partes para calcular la integral ∫xdx, considerando u=x y dv=dx. Entonces, obtenemos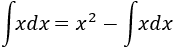

Observad que tenemos la misma integral en ambos lados, así que podemos operar como si fuese una ecuación (como x=a−x, de donde x=a/2), despejando en un lado: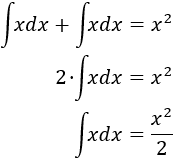

Otros ejemplos de integrales cíclicas: Integral 10, Integral 17 e Integral 19.

No hay que olvidar la constante de integración, C∈R, al final de cada integral.

3.- Imagen