Cambio de variable
Cambio de variable
Samuel Nuñez
Calculo integral
1.- Conocimiento personal.
Por lo que vimos en la clase de este tema, hay algunas integrales que son mucho mas complicadas de resolver por los métodos o reglas conocidas e incluso en algunos no seria posible su solución a no ser que se emplee el uso del método ¨cambio de variable¨.
B) Lo que se me dificulto
Creo que cuando se trata de desmenuzar aun mas a fondo la integral para llegar a obtener una derivada que coincida con la función a la que queremos llegar, ya que en algunos casos es suficiente con intercambiar valores y derivar, en otros casos se alcanza a apreciar que solo requiere simplificar aun mas el resultado dividiendo pero en otros casos mas complicado como el ejemplo que dio el profesor en clase se requiere optar por mas métodos o formas de integrar para obtener su resultado.
2. Conocimiento consultado.
Método de sustitución
El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.

Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable t, de modo que se obtenga una integral más sencilla.
Pasos para integrar por cambio de variable

1 Se hace el cambio de variable y se diferencia en los dos términos:


2Se sutituye la diferencial en la integral:

3 Si la integral resultante es más sencilla, integramos:

4 Se vuelve a la variable inicial:

Ejemplo: Resuelve empleando integración por cambio de variable, la integral

1 Realizamos el cambio de variable

Calculamos la diferencial

2Sustituimos en la integral y simplificamos el integrando

3Resolvemos la nueva integral

4Regresamos a la variable inicial, para ello empleamos 

Así la solución buscada es

Cambios de variables usuales
A continuación enumeramos algunos de los cambios de variables empleados par resolver integrales
1 
2 
3 
4 
5 En las funciones racionales de radicales con distintos índices, de un mismo radicando lineal  , el cambio de variable es
, el cambio de variable es  elevado al mínimo común múltiplo de los índices.
elevado al mínimo común múltiplo de los índices.
6 Si  es par:
es par:
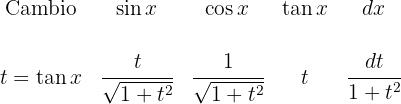
7 Si  no es par:
no es par:

4. Videos
5.- Referencias
Conocimiento consultado: Integración por cambio de variable
Imagenes:
https://es.slideshare.net/slideshow/integracin-por-cambio-de-variable-249550184/249550184



Comentarios
Publicar un comentario